Quantum Models
The quantum calculation of the polarizability, hyperpolarizability and second hyperpolarizability follows along the same lines; but, the dipole moment is replaced with the quantum expectation of the dipole moment, <p>.
Tensor Nature of the Polarizability
When an electric field is applied to a molecule, the induced dipole moment is not necessarily in the direction of the electric field (see the figure below).

Thus, the polarizability is in general a tensor and the dipole moment is related to the electric field according to
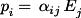
where we use Einstein summation notation, i.e., repeated indices are summed over the three cartesian components. We will use summation notation for the remainder of this tutorial.
The diagonal components of the polarizability represent an induced dipole in the direction of the field while the off-diagonal competes each represent the induced dipole moment perpendicular to the applied field.
Changes in the position of the charges in a material are observed to lag in time relative to the applied external force. Thus, the electric dipole moment induced by an applied electric field will not follow the electric field. In fact, the induced electric dipole may persist for a long time after the electric field is turned off. The diagram below shows a hypothetical response of a molecule.
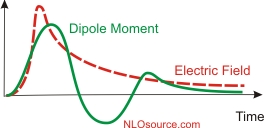
This type of response is called nonlocal in time, which leads to a polarizability whose response is a complex function of the applied electric field. When the response is nonlocal, the induced dipole moment depends on the value of the applied electric field at all times, and can be expressed as,
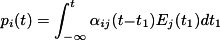 . .
If the response of the molecule were instantaneous, the polarizability tensor would be a delta function in time.
Similarly, the induced dipole moment at one point in a material can depend on the electric field at all other points of the material. When the response in nonlocal spatially, the dipole moment is proportional to an integral over all space of the product of the polarizability and the electric field.
While the treatment of spatial nonlocality is straightforward and parallels the development of time nonlocality, including both makes the equations unwieldy. Furthermore, the effects of spatial nonlocality are usually small. Therefore, we will not describe this case further. However, the reader is warned that spatial nonlocality must be taken into account for certain systems. |
The Hyperpolarizability
To second order in the applied electric field, the nonlocal theory yields the additional term to the induced dipole moment of the form,
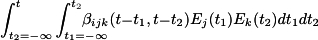
The above equations can be fourier transformed into the frequency domain. When only two monochromatic waves are incident on the molecule, the induced dipole moment reduces to
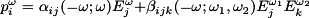
where it is understood that the polarizability and hyperpolarizability, when expressed as a function of frequencies, is the fourier transform of the time domain expression.
In the notation above, the frequency to the left of the semicolon represents the frequency of the dipole oscillation. A negative frequency represents an outgoing wave and a positive frequency an incident wave. Note that because an oscillating dipole leads to dipole radiation, the dipole frequency is negative by convention. By energy conservation, the sums of all the frequency arguments must add to zero.
From the above equation, we can calculate the polarizability from a model of the frequency-dependence using
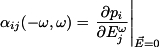
and the hyperpolarizability using
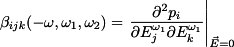
Quantum Mechanical Models
A model of the nonlinear response of a quantum mechanical system requires knowledge of the time dependent wavefunction in the presence of the electric field. Usually, time dependent perturbation theory is used to calculate the wavefunctions using as a basis the wavefunctions of the molecule in the absence of the electric field. (see Quantum model of polarizability (pdf file) for a rigorous treatment.)
Assuming that the wavefunctions in the presence of the electric field are known and of the form
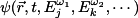 , ,
the charge density will be given by
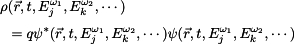 , ,
where q is the electron charge. The dipole moment is then given by
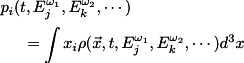
from which the polarizability and hyperpolarizability is calculated by differentiation as defined above.
In ultrashort pulse experiments, the time domain approach is appropriate. When the light source is nearly monochromatic, then one uses the frequency domain response. |